Hello!

This Notebook is associated with the ICASSP2022 submission, presenting audio outputs of the Nonnegative Tucker Decomposition (NTD) when optimizing different loss functions. In particular, the three evaluated loss functions are three special cases of the more general $\beta$-divergence:

• The Euclidean norm, $\beta = 2$,
• The Kullback-Leibler (KL) divergence, $\beta = 1$,
• The Itakura-Saito (IS) divergence, $\beta = 0$.

More details about our algorithm are to be found in the ICASSP submsission (which should be the reason of your presence on this page). Audio signals are obtained by applying the Griffin-Lim algorithm to STFT.

This notebook will present signals, showing results of:

• The Griffin-Lim algortihm itself, by recomposing the phase of the original STFT of the song, to serve as a baseline for the other estimations. This baseline condition already presents some artifacts on the reconstructed signal.
• A comparison of the decomposition results with the three different loss functions. This comparison is obtained by omparing:
  • The reconstructed song itself, result of the whole decomposition,
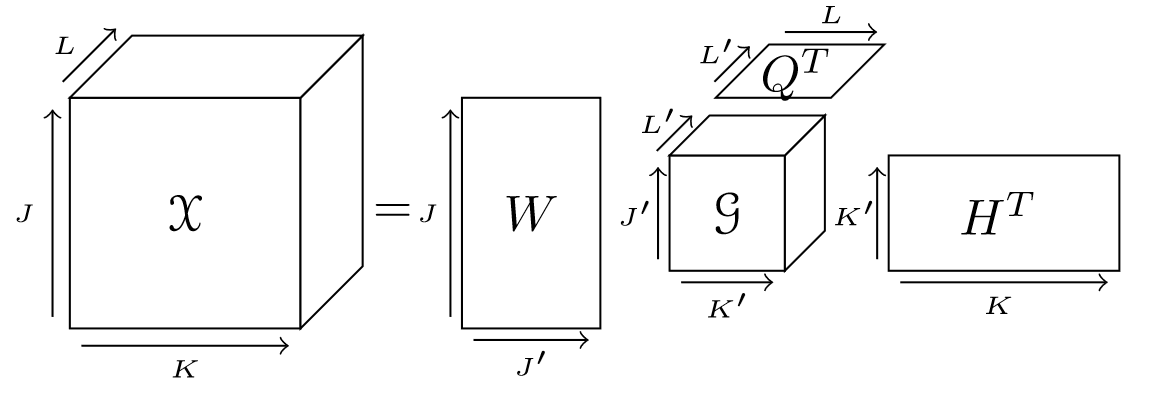
  • The different patterns ($W G_{[:,:,i]} H^T$, with $i$ the pattern index), obtained by the decomposition.

Note though that signals representing songs will be limited to the first 16 bars, in order to limit the size of this HTML page.

We insist on the fact that, while audio signals are listenable, they are not of profesional musical quality either due to inaccuracies in the decomposition or due to the phase-estimation algorithm that we use (Griffin-Lim). Improving the reconstruction of these signals could constitute future work.

In the meantime, we believe that these audio examples are good examples of the potential and outputs of the NTD, and allow to qualitatively evaluate the differences between the different loss functions.

Imports

Let's start with importing external librairies (which are installed automatically if you used pip install, otherwise you should install them manually).

# External imports
# Module for manipulating arrays
import numpy as np

# Module for loading signals
import soundfile as sf

# Module for manipulating signals, notably 
import librosa

import IPython.display as ipd

And now, let's import the nn_fac and MusicNTD code (respectively code for Nonnegative Factorizations methods and for everything else (data manipulation, segmentation, etc) associated with NTD for music segmenation):

# Module containing our NTD resolution algorithm
import nn_fac.ntd as NTD

# Module encapsulating the computation of features from the signal
import musicntd.model.features as features

# General module for manipulating data: conversion between time, bars, frame indexes, loading of data, ...
import musicntd.data_manipulation as dm

# Module constructing the tensor, starting from the spectrogram
import musicntd.tensor_factory as tf

# Plotting module
from musicntd.model.current_plot import *

Next, we need to load the song to decompose. We used Come Together from The Beatles as example, but feel free to chose any song you'd like! (in wav though.)

NB: this comment only applies of you're compiling the Notebook, and not reading the HTML, as the HTML is static.

# Song
song_path = "C:/Users/amarmore/this_folder/The Beatles - Come Together.wav"
the_signal, sampling_rate = sf.read(song_path)

# Get the downbeats
bars = dm.get_bars_from_audio(song_path)

C:\Users\amarmore\AppData\Local\Continuum\anaconda3\envs\NTD_segmentation\lib\site-packages\scipy\io\wavfile.py:273: WavFileWarning: Chunk (non-data) not understood, skipping it.
  WavFileWarning)

STFT

Let's compute the STFT of the song:

n_fft=2048
hop_length = 32

stft_complex = librosa.core.stft(np.asfortranarray(the_signal[:,0]), n_fft=n_fft, hop_length = hop_length)
for i in range(1,the_signal.shape[1]):
    stft_complex += librosa.core.stft(np.asfortranarray(the_signal[:,i]), n_fft=n_fft, hop_length = hop_length)
mag, phase = librosa.magphase(stft_complex, power=1) # Magnitude spectrogram

and then form the tensor-spectrogram of this STFT:

hop_length_seconds = hop_length / sampling_rate
subdivision = 96

tensor_stft = tf.tensorize_barwise(mag, bars, hop_length_seconds, subdivision)

We reconstruct the song from the unfolded tensor spectrogram. Hence, the song will be reconstructed from the 96 chosen samples per bar.

To reconstruct the song, the algorithm needs the hop length of the STFT. As bars can be of different length, we compute the median hop length from the different bars, and applies it to all bars in our song.

hops = []
for bar_idx in range(tensor_stft.shape[2]):
    len_sig = bars[bar_idx+1][1] - bars[bar_idx+1][0]
    hop = int(len_sig/96 * sampling_rate)
    hops.append(hop)
median_hop = int(np.median(hops))

Now, let's recreate the signal from the barwise STFT, in order to study the reconstruction quality of the Griffin-Lim algorithm. We limit the song to a certain number of bars (not to overload the final HTML file).

nb_bars = 16 # you can set it to 89 if you use the executable format, and listen to the whole song.
time = nb_bars * subdivision
audio_stft = librosa.griffinlim(np.reshape(tensor_stft[:,:,:nb_bars], (1025, time), order = 'F'), hop_length = median_hop)

Let's hear it:

ipd.Audio(audio_stft, rate=sampling_rate)